The large LLMs of the world today, even with all the sophistication, still have no concept of real memory. Developers create the illusion of memory by increasing the amount of data that the LLM can process at a time (context length). In these cases, the LLM will not ‘remember’ a user conversation even from a couple days ago. The solution thought up by the brightest minds was to store past conversations and other relevant information directly in a database; & push it to the LLM when it is needed. This concept is called Retrieval Augmented Generation (RAG). We can see the glaring problem here. How do you search & retrieve the appropriate text or image or audio from the database? The naive solution is to index everything (like keyword search in Google). With keyword search we only capture documents with the exact words. For example if we search for ‘doctor salary’ , we might miss documents with the words ‘physician compensation’. For this reason, we design search systems to capture semantic meaning. By converting our document to an ‘embedding’ vector (or group of vectors), users can phrase their questions in any way and our search algorithm will be able to find relevant documents.

We have converted our large corpus of text (& images, audio, etc.) to vectors & stored them in our database. Now how do we search for the relevant vectors? We can transform the user’s question into a vector & search our database for the top 10 vectors closest to the user’s question vector. Great! problem solved. Not quite, in a database with billions (or trillions) of vectors; we would have to compare the user’s vector with each of the vectors in our DB. Imagine the time it would take to run that search. Not good. It would take days to get a response from the LLM. Exact nearest vector methods are prohibitive but there are many approximate nearest algorithms that are faster ie. graph-based (HNSW), hash-based (Locality Sensitive Hashing), etc. Currently the go-to method for production systems (like Milvus, FAISS, etc.) is HNSW. Even this algorithm’s time complexity is log(N), where N is the total no. of vectors in our DB. Even for highly optimized systems, it can take 100s of milliseconds for every search. Is there any way we can make it faster?

Quantization to the rescue. Instead of storing the vector in the original 32 bit floating point representation, why not bring the size down to 16 bits or 8 bits. We get a 4x compression with 8 bit quantization. Instead of storing 1536 float32 values (≈6 KB per vector), you might just store <1 KB. Smaller memory footprint means vectors will fit in CPU/GPU caches. Fetching them from memory would be much faster. Searches become faster since we can perform faster calculations on smaller-sized vectors. But there is a downside, by reducing the size from 32 bit to 8 bit, we lose some precision in the numbers. If we were to quantize a 32 bit vector down to 8bits and then bring it back up to 32 bits (to feed to the LLM) ; we won’t get back our original vector but a vector with rounded-off values. There will alway be some loss in information due to quantization. The losses become larger if some elements of the vectors have higher ranges than others. Some vector dimensions may have uneven distributions (e.g., one dimension has a wide range of values while another barely varies). If we naively quantize directly, these “dominant” dimensions can introduce larger rounding errors. Larger errors due to quantization might distort the distances between vectors. Our Nearest Vector search algorithm might not return the nearest vector. A simple solution is to rotate the vectors to distribute the variance across all the dimensions. A rotation spreads the information more evenly across all dimensions, making quantization errors more uniform.

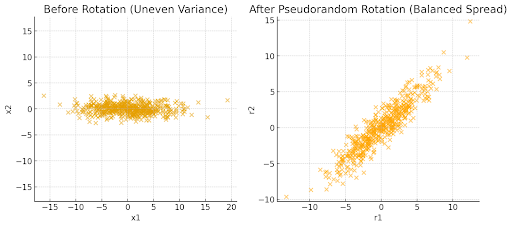
In the image, before rotation, the vectors are stretched mostly along the x-axis, so one dimension dominates. After the rotation, the vectors are spread more evenly across both axes, making quantization errors more uniform. The rotation matrix is generated once, using a random seed or deterministic algorithm. The rotation is orthogonal (preserves distances and angles before quantization). Every vector gets rotated in the same way. Even though each vector is rotated, the relative distances between vectors remain unchanged (before quantization). Since the rotation is linear, the relative distances between vectors is also unchanged.

I ran a simulation to compare vector search recall for naive quantization, pseudo-random rotational quantization (and a foolish PCA based rotation quantization). The simulations run 30 times for each vector length (increasing in multiples of 10, from 10 to 300) to capture the mean recall for all 3 quantization methods.

I plotted the vector search recall@5 against vector lengths (dimensions) for naive, pseudo random & PCA based rotation. (Here’s the colab notebook)

The x-axis lists the vector lengths (dimension), y-axis shows recall.

This plot shows recall against vector-lengths for normally distributed data. Since there are no varying dimensions in the vectors, the naive and pseudo random quantization recalls are very close.

This plot shows recall against vector-lengths for data where the means of each vector dimension has differing means. (ex. for vector length 20, dim 12 might be sampled from normal distribution with mean 9, dim 15 from dist. with mean 3). Since the variances in the vectors are almost constant, the naive and pseudo random quantization recalls are very close.

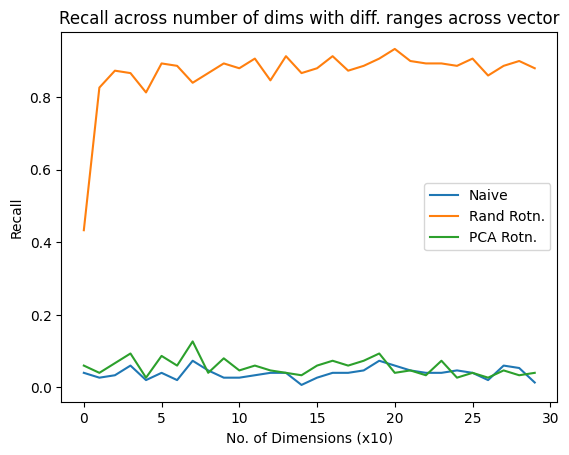
This plot shows recall against vector-lengths for data where 10% of the vector dimensions have extremely large range of values. For example, vector length 20, atleast 2 dimensions will have ranges of [-200,200]. The variances in the vectors are quite large, we can see that rotational quantization performs exceedingly well compared to naive quantization. Naive quantization fails for most cases.

From the plots, it is quite clear that Rotational Quantization should be the preferred quantization method if the vector dimension ranges are not constant.